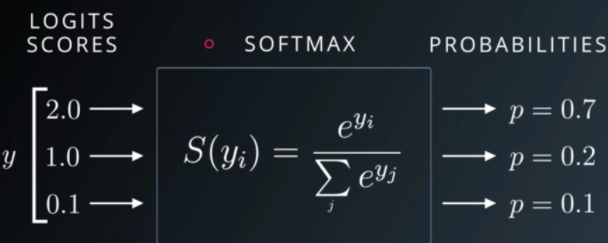Neuronale Netze | Blogs | Kasem Rashrash

Ich musste im Fach Mathematik eine Präsentation halten. Ich dachte an KI, denn das Thema ist aktuell, spannend, und ich wollte verstehen, wie dort eigentlich Mathematik verwendet wird. Und genau das habe ich entdeckt! In diesem Beitrag zeige ich euch die Lernschritte, die ich gemacht habe, und was ich über Wahrscheinlichkeiten in neuronalen Netzen verstanden habe:

Was sind neuronale Netze überhaupt?

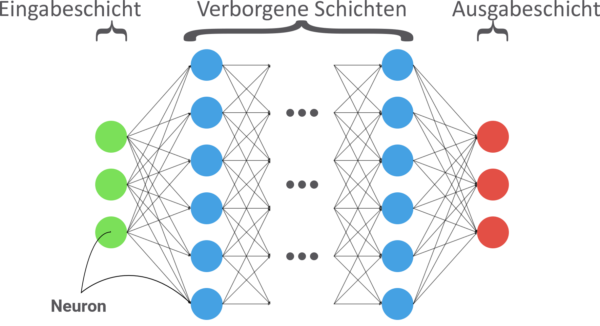
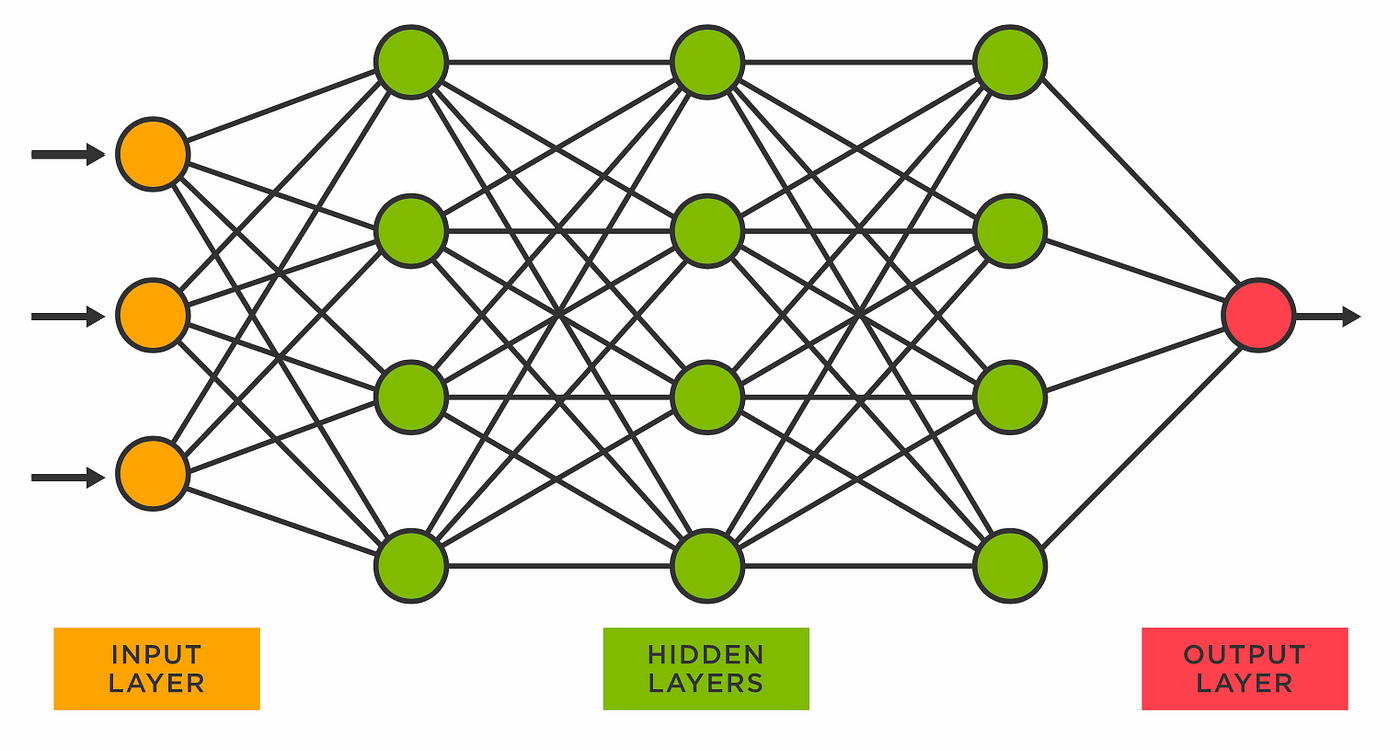
Ein neuronales Netz besteht aus künstlichen "Neuronen", die in Schichten organisiert sind: Eingabeschicht, versteckte Schichten und Ausgabeschicht. Es funktioniert ähnlich wie unser Gehirn: Daten kommen rein, werden gewichtet, summiert, durch Funktionen gejagt und am Ende kommt eine Entscheidung heraus. Das Besondere: Diese Entscheidung ist keine 100% Ja/Nein-Antwort, sondern eine Wahrscheinlichkeit.

Warum Wahrscheinlichkeit?

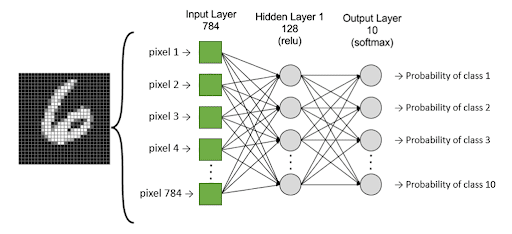
In der KI besonders bei der Bildverarbeitung oder Spracherkennung geht es oft darum: „Wie wahrscheinlich ist es, dass dies eine 6 ist?“ oder „Wie sicher ist die KI, dass hier ein Tumor zu sehen ist?“
Statt Schwarz-Weiß-Antworten werden Wahrscheinlichkeiten berechnet. Zum Beispiel: „Mit 82,3 % Wahrscheinlichkeit ist ein Tumor vorhanden.“

So entsteht eine Wahrscheinlichkeit im Netz

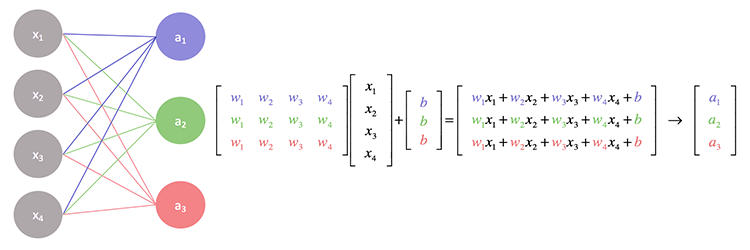
Jeder Inputwert (z. B. ein Pixelwert aus einem Bild) wird mit einem Gewicht w multipliziert, dann alles aufsummiert und ein sogenannter Bias b hinzugefügt. Die Formel dafür ist:

z = Σ (wᵢ * xᵢ) + b

Anschließend wird dieser Wert durch eine Aktivierungsfunktion geschickt. Zwei wichtige Funktionen sind:

1. Sigmoid-Funktion

Gibt einen Wert zwischen 0 und 1 zurück.

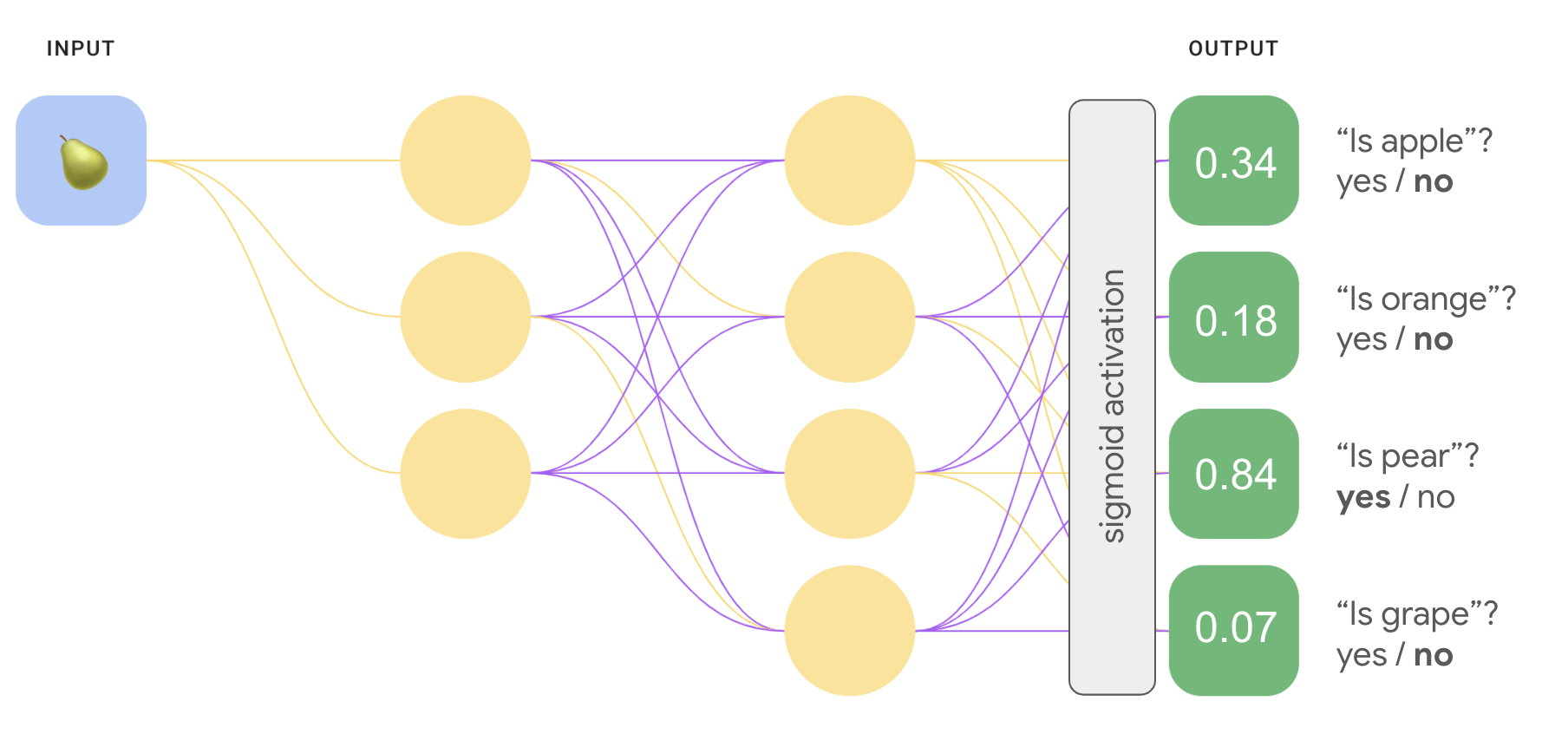
Beispiel: Bei z = 1.54 ergibt sich sigmoid(z) ≈ 0.823 → Die Wahrscheinlichkeit beträgt ca. 82,3 %.

2. Softmax-Funktion

Wenn es mehrere Klassen gibt (z. B. Zahl 0–9), wandelt Softmax alle Ausgaben so um, dass sie zwischen 0 und 1 liegen und zusammen 1 ergeben. Beispiel in Python:

import numpy as np

def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum()

softmax([2.0, 1.0, 0.1])
# Output: [0.659, 0.242, 0.099]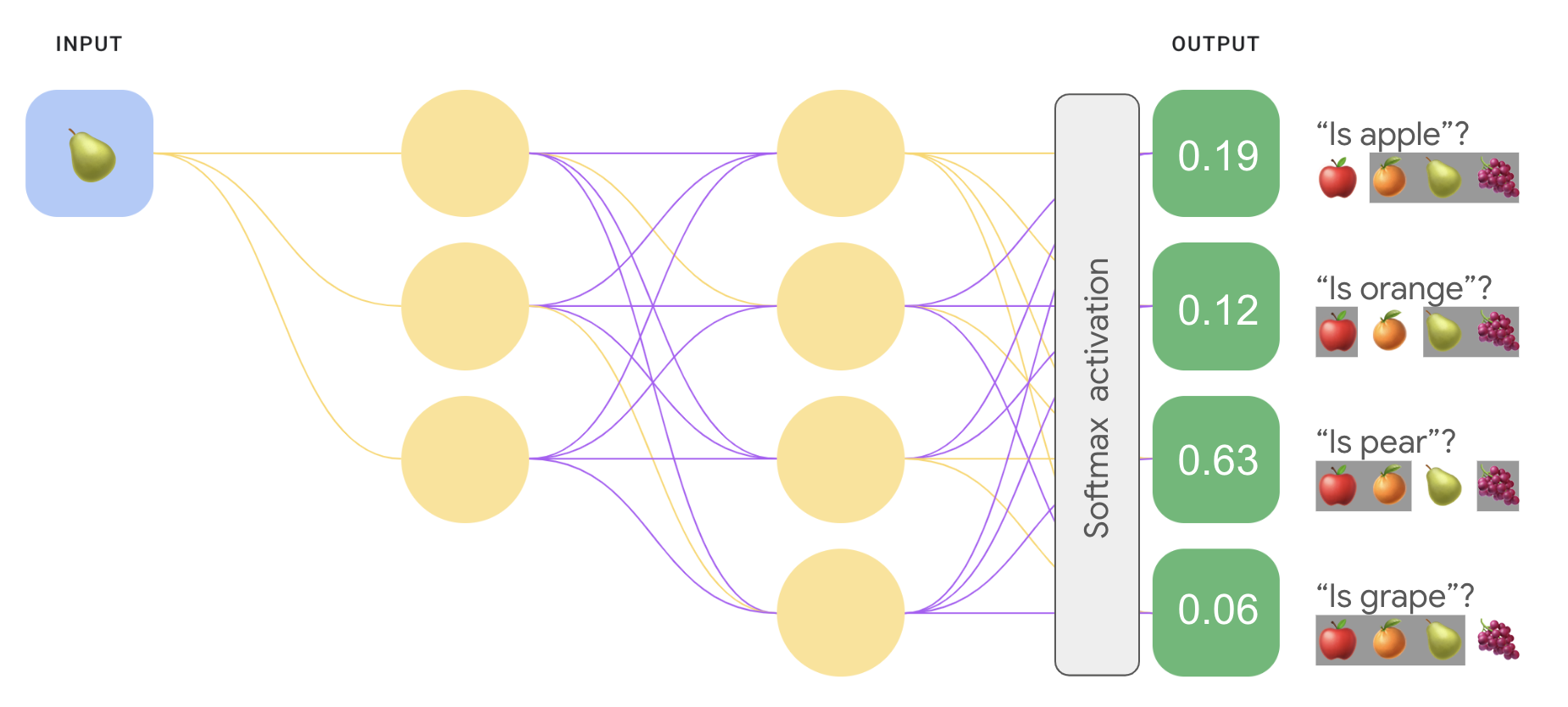

Beispiel: Tumorerkennung

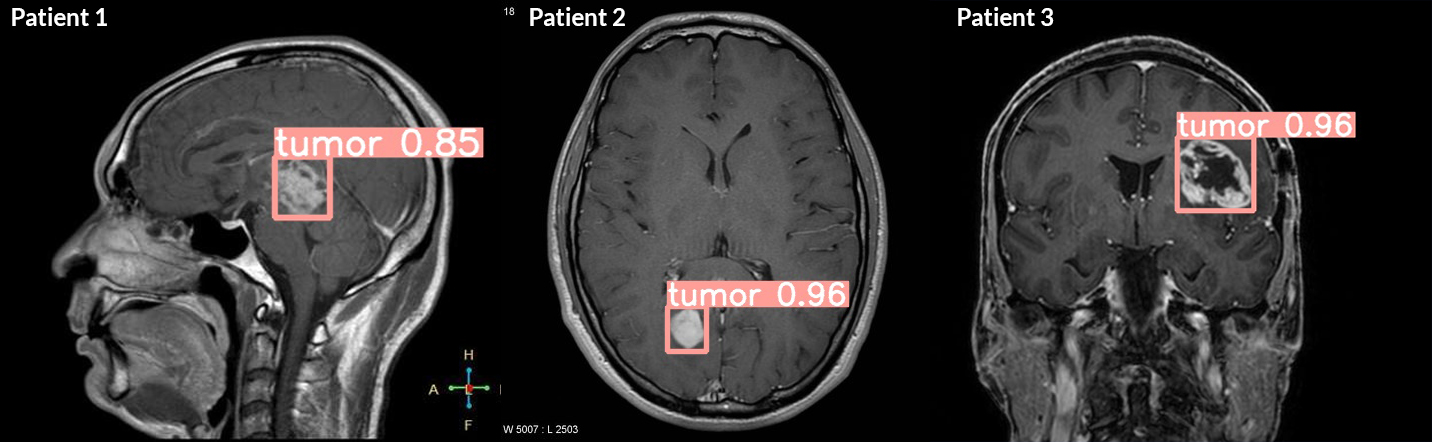
Ein neuronales Netz wird mit MRT-Bildern trainiert und erkennt mit z. B. 0.96 Wahrscheinlichkeit, dass ein Tumor vorhanden ist. Je höher der Wert, desto sicherer ist das Modell:

Patient 1: 0.85 → Tumor erkannt
Patient 2: 0.98 → Tumor erkannt
Patient 3: 0.96 → Tumor erkannt

Wie lernt das Netz?

Beim Training vergleicht das Netz seine Vorhersage mit der echten Antwort („Ground Truth“) und berechnet den Fehler (Loss). Bei binären Entscheidungen z. B. mit der Kreuzentropie:

Loss = - (y * log(ŷ) + (1 - y) * log(1 - ŷ))

Beispiel: y = 1, ŷ = 0.823 → Loss ≈ 0.195

Dann passt das Netz seine Gewichte mit dem Verfahren Backpropagation an:

w = w - η * ∂Loss/∂w

Fazit

Mathe steckt wirklich überall drin und in neuronalen Netzen sieht man das ganz direkt: Wahrscheinlichkeiten entstehen durch Summen, Gewichte, Aktivierungsfunktionen und Optimierung. Was ich besonders spannend fand: Das Netz lernt selbst aus seinen Fehlern und das durch pures Rechnen.

Für mich war es eine perfekte Verbindung aus Informatik und Mathematik. Ich habe erkannt, dass KI nicht einfach „magisch“ ist, sondern auf logischen und mathematisch erklärbaren Prinzipien beruht. Sie analysiert Daten, berechnet Wahrscheinlichkeiten und trifft Entscheidungen auf Basis von gelernten Mustern.

Besonders wichtig ist mir aber der Gedanke, dass KI nicht dazu da ist, Menschen zu ersetzen, sondern sie zu unterstützen. In der Tumorerkennung zum Beispiel kann eine KI-Analyse Ärztinnen und Ärzte bei der Diagnose schneller helfen, objektiver und auf Basis großer Datenmengen. Die letzte Entscheidung bleibt aber immer beim Menschen.

Dieses Projekt hat mir gezeigt: Wenn man versteht, wie neuronale Netze funktionieren, verliert man die Angst vor dem Unbekannten und kann sogar selbst mitgestalten, wie die KI von morgen aussieht.